

Reinforcement Learning

Reinforcement learning is learning what to do—how to map situations to actions—so as to maximize a numerical reward signal. The learner is not told which actions to take, but instead must discover which actions yield the most reward by trying them.

• A policy defines the learning agent’s way of behaving at a given time. Roughly speaking, a policy is a mapping from perceived states of the environment to actions to be taken when in those states.
• A reward signal defines the goal of a reinforcement learning problem. On each time step, the environment sends a single number called the reward to the reinforcement learning agent.
• The reward signal indicates what is good in an immediate sense, a value function specifies what is good in the long run. Roughly speaking, the value of a state is the total amount of reward an agent can expect to accumulate over the future, starting from that state.
• Model mimics the behavior of the environment, or more generally, that allows inferences to be made about how the environment will behave.

Methods for solving reinforcement learning problems that use models and planning are called model-based methods, as opposed to simpler model-free methods that are explicitly trial-and-error learners.

Reinforcement learning uses the formal framework of Markov decision processes to define the interaction between a learning agent and its environment in terms of states, actions, and rewards. We will learn problem formulation with finite Markov Decision Processes and its main ideas including Bellman equations and value functions.

Three fundamental classes of methods for solving finite Markov decision problems:

• Dynamic programming
• Monte Carlo methods
• Temporal difference learning

The methods also differ in several ways with respect to their efficiency and speed of convergence.

Dynamic programming methods are well developed mathematically, but require a complete and accurate model of the environment.

Monte Carlo methods don’t require a model and are conceptually simple, but are not well suited for step-by-step incremental computation.

Temporal-difference methods require no model and are fully incremental, but are more complex to analyze.

If actions are allowed to affect the next situation as well as the reward, then we have the full reinforcement learning problem.

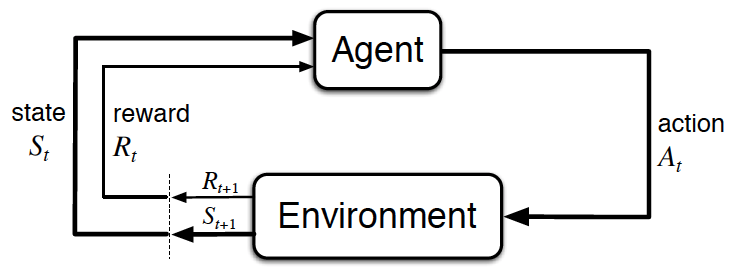
• The learner and decision maker is called the agent.
• The thing it interacts with, comprising everything outside the agent, is called the environment.
• Thus RL framework is characterized by an agent learning to interact with its environment.
• At each time step, the agent receives the environment's state (the environment presents a situation to the agent), and the agent must choose an appropriate action in response. One time step later, the agent receives a reward (the environment indicates whether the agent has responded appropriately to the state) and a new state.
• All agents have the goal to maximize expected cumulative reward, or the expected sum of rewards attained over all time steps.

The state must include information about all aspects of the past agent–environment interaction that make a difference for the future. If it does, then the state is said to have the Markov property.

Episodic vs. Continuing Tasks

• A task is an instance of the reinforcement learning (RL) problem.
• Continuing tasks are tasks that continue forever, without end.
• Episodic tasks are tasks with a well-defined starting and ending point.
  • In this case, we refer to a complete sequence of interaction, from start to finish, as an episode.
  • Episodic tasks come to an end whenever the agent reaches a terminal state.

The Reward Hypothesis

• Reward Hypothesis: All goals can be framed as the maximization of (expected) cumulative reward.

Cumulative Reward

The return at time step t is $$G_t := R_{t+1} + R_{t+2} + R_{t+3} + \ldots$$ The agent selects actions with the goal of maximizing expected (discounted) return.

Discounted Return

• Discounting: The agent tries to select actions so that the sum of the discounted rewards it receives over the future is maximized.
• The discounted return at time step t is $$G_t := R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \ldots$$ $$G_t = R_{t+1} + \gamma (R_{t+2} + \gamma R_{t+3} + \ldots)$$ $$G_t = R_{t+1} + \gamma G_{t+1}$$ $$G_t = \sum_{k=0}^\infty \gamma^k R_{t+k+1}$$
• The discount rate $\gamma$ is something that you set, to refine the goal that you have the agent.
  • It must satisfy 0 <= $\gamma$ <= 1
  • If $\gamma=0$, the agent only cares about the most immediate reward.
  • If $\gamma=1$, the return is not discounted.
  • For larger values of $\gamma$, the agent cares more about the distant future. Smaller values of $\gamma$ result in more extreme discounting, where - in the most extreme case - agent only cares about the most immediate reward.

MDPs and One-Step Dynamics

• The state space $\mathcal{S}$ is the set of all (nonterminal) states.
• In episodic tasks, we use $\mathcal{S}^+$ to refer to the set of all states, including terminal states.
• The action space $\mathcal{A}$ is the set of possible actions. (Alternatively, $\mathcal{A(s)}$ refers to the set of possible actions available in state $s \in (\mathcal{S}$
• The one-step dynamics of the environment determine how the environment decides the state and reward at every time step. The dynamics can be defined by specifying

$$p(s',r|s,a) \doteq \mathbb{P}(S_{t+1}=s', R_{t+1}=r|S_{t} = s, A_{t}=a) \text{ for each possible } s', r, s, \text{and } a$$

• A (finite) Markov Decision Process (MDP) is defined by:
  • a (finite) set of states $\mathcal{S}$ (or $\mathcal{S}^+$, in the case of an episodic task)
  • a (finite) set of actions $\mathcal{A}$
  • a set of rewards $\mathcal{R}$
  • the one-step dynamics of the environment
  • the discount rate $\gamma \in [0,1]$

Bellman Equations

In this gridworld example, once the agent selects an action,

• it always moves in the chosen direction (contrasting general MDPs where the agent doesn't always have complete control over what the next state will be), and
• the reward can be predicted with complete certainty (contrasting general MDPs where the reward is a random draw from a probability distribution).

In this simple example, we saw that the value of any state can be calculated as the sum of the immediate reward and the (discounted) value of the next state.

Alexis mentioned that for a general MDP, we have to instead work in terms of an expectation, since it's not often the case that the immediate reward and next state can be predicted with certainty. Indeed, we saw in an earlier lesson that the reward and next state are chosen according to the one-step dynamics of the MDP. In this case, where the reward r and next state s′ are drawn from a (conditional) probability distribution $p(s',r|s,a)$, the Bellman Expectation Equation (for $v_\pi)$ expresses the value of any state s in terms of the expected immediate reward and the expected value of the next state:

$$v_\pi(s) = \mathbb{E}_\pi[R_{t+1} + \gamma v_\pi(S_{t+1})|S_t =s]$$

Calculating the Expectation

In the event that the agent's policy π is deterministic, the agent selects action $\pi(s)$ when in state $s$, and the Bellman Expectation Equation can be rewritten as the sum over two variables ($s′ \text{ and } r$):

$$v_\pi(s) = \text{} \sum_{s'\in\mathcal{S}^+, r\in\mathcal{R}}p(s',r|s,\pi(s))(r+\gamma v_\pi(s'))$$

In this case, we multiply the sum of the reward and discounted value of the next state $(r+\gamma v_\pi(s'))$ by its corresponding probability $p(s',r|s,\pi(s))$ and sum over all possibilities to yield the expected value.

If the agent's policy $\pi$ is stochastic, the agent selects action $a$ with probability $\pi(a∣s)$ when in state $a$, and the Bellman Expectation Equation can be rewritten as the sum over three variables $(s′, r, a)$:

$$v_\pi(s) = \text{} \sum_{s'\in\mathcal{S}^+, r\in\mathcal{R},a\in\mathcal{A}(s)}\pi(a|s)p(s',r|s,a)(r+\gamma v_\pi(s'))$$

In this case, we multiply the sum of the reward and discounted value of the next state $(r+\gamma v_\pi(s'))$ by its corresponding probability $π(a∣s)p(s′,r∣s,a)$ and sum over all possibilities to yield the expected value.

Policies

• A deterministic policy is a mapping $\pi: \mathcal{S}\to\mathcal{A}$. For each state $s \in S$, it yields the action (a \in A) that the agent will choose while in state $s$.

• A stochastic policy is a mapping $\pi: \mathcal{S}\times\mathcal{A}\to [0,1]$. For each state $s \in S$ and action $a \in A$, it yields the probability $\pi(a|s)$ that the agent chooses action $a$ while in state $s$.

State-Value Functions

• The state-value function for a policy $\pi$ is denoted $v_\pi$. For each state $s \in S$, it yields the expected return if the agent starts in state $s$ and then uses the policy to choose its actions for all time steps. That is,

$$v_\pi(s) \doteq \mathbb{E}_\pi[G_t | S_t=s]$$ We refer to $v_\pi(s)$ as the value of state $s$ under policy $\pi$.

• The notation $\mathbb{E}_\pi[\cdot]$ denotes the expected value of a random variable given that the agent follows policy $\pi$, and $t$ is any time step.

Optimality

• A policy $\pi′$ is defined to be better than or equal to a policy $\pi$ if and only if $v_{\pi'}(s) \geq v_\pi(s)$ for all $s \in S$.

• An optimal policy $\pi_*$ satisfies $\pi_*\ge\pi$ for all policies π. An optimal policy is guaranteed to exist but may not be unique.

• All optimal policies have the same state-value function $v_*$ called the optimal state-value function.

Action-Value Functions

• The action-value function for a policy $\pi$ is denoted $q_\pi$. For each state $s \in S$ and action $a \in A$, it yields the expected return if the agent starts in state $s$, takes action $a$, and then follows the policy for all future time steps. That is,

$$q_\pi(s,a) \doteq \mathbb{E}_\pi[G_t|S_t=s, A_t=a]$$

We refer $q_\pi(s,a)$ as the value of taking action $a$ in state $s$ under a policy $\pi$ (or alternatively as the value of the state-action pair s,a).

• All optimal policies have the same action-value function $q_*$, called the optimal action-value function.

Optimal Policies

• Once the agent determines the optimal action-value function $q_*$, it can quickly obtain an optimal policy $\pi_*$ by setting:

$$\pi_*(s) = \arg\max_{a\in\mathcal{A}(s)} q_*(s,a)$$